طريقة حساب مساحة المثلث مختلف الأضلاع
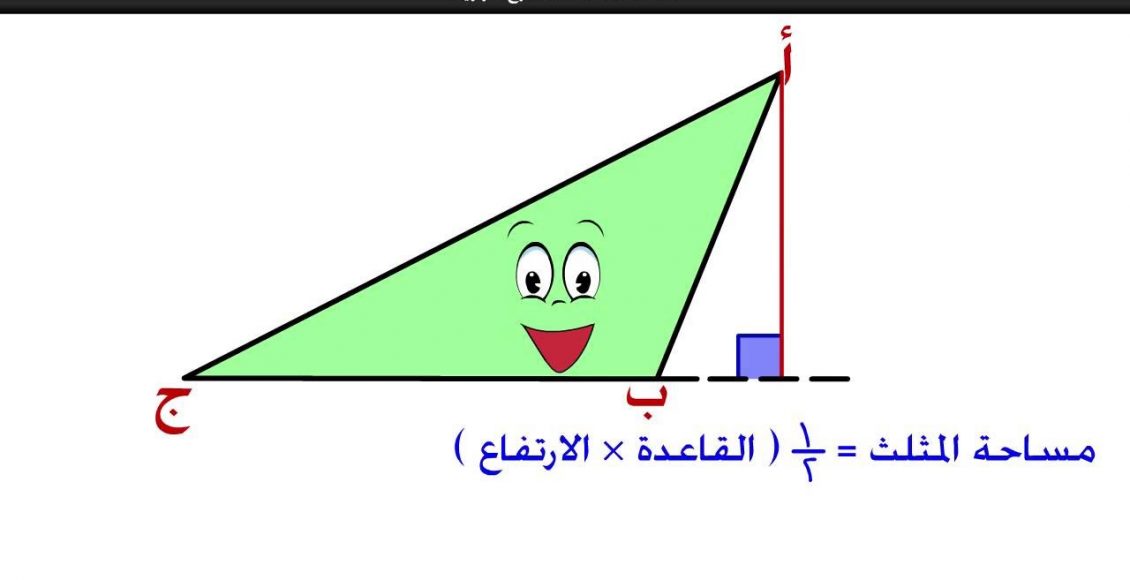
مساحة المثلث مختلف الأضلاع يعتبر المثلث مختلف الأضلاع نوع من أنواع من المثلثات التي تختلف فيها أطوال أضلاعه الثلاث، ويمكن حساب مساحة المثلث مختلف الأضلاع بعدة طرق منها طريقة العد، أو بواسطة تطبيق قانون حساب مساحة المثلث، ويعرف المثلث بأنه شكل هندسي ثنائي الأبعاد، توجد منه أنواع عديدة منها المثلث المتساوي الساقين و المثلث المختلف الأضلاع و المثلث المتساوي الأضلاع.
أنواع المثلث
المثلث هو واحد من الأشكال الهندسية المغلقة التي تتميز بوجود ثلاث رؤوس تسمي الزوايا، و ثلاث أضلاع عبارة عن قطع مستقيمة متصلة ليست في مستوى واحد، ويمكن تقسيم المثلث إلى ثلاثة أنواع مختلفة حسب عاملين إما أطوال الأضلاع أو أنواع الزوايا كما يلي:
أنواع المثلث حسب أطوال أضلاعه
- مثلث مختلف الاضلاع وتكون فيه أضلاعه مختلفة في الطول.
- مثلث متساوي الساقين ويتساوى فيها طول ضلعين والثالث مختلف.
- النوع الثالث يكون متساوي الأضلاع حيث تتساوى فيه أطوال أضلاعه الثلاثة.
أنواع المثلث حسب زواياه
- مثلث حاد الزوايا وتكون جميع الزوايا فيه حادة .
- مثلث قائم الزاوية وتكون إحدى زواياه الثلاث قائمة والزاويتين الثانيتين حادتين.
- مثلث منفرج الزاوية وتكون فيه أحد الزوايا منفرجة والأخيرتين حادتين.
ومن هنا يمكنكم قراءة موضوع المساحة الجانبية لمتوازي المستطيلات وحجمه ومحيطه: المساحة الجانبية لمتوازي المستطيلات وحجمه ومحيطه
خواص المثلث مختلف الأضلاع
يتميز هذا النوع من المثلثات بعدة خصائص هي :
- تكون أطوال أضلاعه الثلاثة مختلفة في الطول.
- يتميز بأن قيمة الزوايا الثلاثة للمثلث مختلفة.
- عند القيام بجمع قيم أطوال أي ضلعين في المثلث تكون دائما أكبر من قيمة طول الضلع الثالث.
- يتميز بأن مجموع قيم زواياه الثلاث يقدر ب 180درجة
- عند جمع أي زاويتين من زوايا المثلث، فإن الناتج يساوي دائما قيمة الزاوية الخارجة لهذا المثلث.
حساب مساحة المثلث مختلف الأضلاع
يتم حساب المساحة المحصورة بين أضلاع المثلث بعدة طرق مختلفة منها
استخدام طريقة عد المربعات
يتم في هذه الطريقة تقسيم سطح المثلث إلي مربعات صغيرة يبلغ طول ضلع المربع حوالي ١سم، يتم بعد ذلك القيام بعد المربعات المحصورة بين أضلاع المثلث الثلاث، ويكون الناتج هو قيمة مساحة المثلث.
استخدام قانون حساب مساحة المثلث
لكي يتم استخدام قانون حساب مساحة المثلث في حساب مساحة المثلث مختلف الأضلاع لابد من تحقيق الشروط التالية
- ضرورة معرفة أحد أطوال أضلاعه، وهو القاعدة
- معرفة طول العمود المقام من الزاوية المقابلة لهذه القاعدة، والذي يطلق عليه الارتفاع.
- ينص القانون العام على أن تقدر مساحة المثلث = 1/2 طول القاعدة×ارتفاع المثلث.
مثال على ذلك
احسب مساحة المثلث مختلف الأضلاع إذا علمت أن طول قاعدته يساوي 7 سم وارتفاعه يساوي 10 سم.
الحل: باستخدام القانون: مساحة المثلث = 1/2× طول القاعدة ×الارتفاع =1/2×10×7 =35 سم²
ومن هنا سنتعرف علي موضوع قانون مساحة متوازي الاضلاع وخصائصه ومميزاته والحالات الخاصة في متوازي الأضلاع: قانون مساحة متوازي الاضلاع وخصائصه ومميزاته والحالات الخاصة في متوازي الأضلاع
حساب مساحة مثلث مختلف الأضلاع بمعلومية طول ضلعين وزاوية
يعتبر المثلث مختلف الأضلاع نوع من أنواع المثلثات، لذلك يمكن حساب مساحته بمعرفة أطوال أضلاعه الثلاثة باستخدام القوانين التالية
أولا
مساحة المثلث مختلف الأضلاع = ½طول الضلع الأول ×طول الضلع الثاني × جا س، حيث تعبر س عن الزاوية الموجودة بين كلا من الضلع الأول والثاني.
ثانيا
مساحة المثلث = ½ طول الضلع الثاني×الضلع الثالث× جا ص، حيث تعتبر ص هي الزاوية الواقعة بين الضلع الثالث والضلع الثاني.
ثالثا
مساحة المثلث =½ طول الضلع الأول × طول الضلع الثالث ×جا ع، حيث ترمز ع الزاوية بين الضلعين الأول والثالث.
رابعا
باستخدام القانون العام مساحة المثلث =1/2× طول القاعدة × ارتفاع المثلث.
ولا يفوتكم قراءة موضوع مساحة المثلث القائم الزاوية ونظرية فيثاغورث في المثلث القائم الزاوية: مساحة المثلث القائم الزاوية ونظرية فيثاغورث في المثلث القائم الزاوية
حساب مساحة المثلث مختلف الأضلاع بمعلومية أطوال أضلاعه
يمكن حساب مساحة المثلث مختلف الأضلاع بمعرفة أطوال أضلاعه عن طريق الآتي:
- القيام بحساب محيط المثلث باستخدام القانون محيط المثلث = مجموع أطوال أضلاعه
- القيام بحساب المعامل ه حيث ه= المحيط /2.
- تطبيق العلاقة التالية : المساحة = الجذر التربيعي (ه(ه_(طول الضلع الأول )(هو(طول الضلع الثاني)(هو(طول الضلع الثالث))
مثال
احسب مساحة مثلث أطوال أضلاعه تساوي 6 سم، 8 سم، 4 سم على الترتيب.
الحل محيط المثلث =6+8+4=18سم³، والمعامل هـ=18/2=9 سم
- باستخدام قانون مساحة المثلث = الجذر التربيعي(ه(ه_(طول الضلع الأول )(هو(طول الضلع الثاني)(هو(طول الضلع الثالث))
- مساحة المثلث=الجذر التربيعي(9(9-8)(9-4)(9-6))=الجذر التربيعي 9*1*5*3=135√سم²
وللتعرف علي موضوع ما هو محيط المثلث؟ والقانون العام لمحيط المثلث: ما هو محيط المثلث؟ والقانون العام لمحيط المثلث
أمثلة متنوعة على حساب مساحة المثلث مختلف الأضلاع
مثال رقم (1)
إذا علمت أن أطوال أضلاع مثلث على التوالي يساوي 5 سم، 7 سم، 4 سم، احسب مساحته
الحل باستخدام قانون مساحة المثلث = الجذر التربيعي(ه(ه_(طول الضلع الأول )(هو(طول الضلع الثاني)(هو(طول الضلع الثالث))
- محيط المثلث=5+7+4=16
- المعامل ه =16/2=8
- مساحة المثلث= الجذر التربيعي (8(8-5)(8-7)(8-4) = الجذر التربيعي 8*3*1*4 =96√
مثال رقم (2)
احسب مساحة مثلث مختلف الأضلاع، إذا عرفت أن طول قاعدته٩سم وارتفاعه ١٢سم
الحل باستخدام العلاقة مساحة المثلث متساوي الأضلاع =1/2× القاعدة × الارتفاع = 1/2×9×12= 54سم²
مثال رقم (3)
مثلث مختلف الأضلاع وارتفاعه 6 سم، وطول قاعدته 3 سم احسب مساحته
الحل مساحة المثلث=1/2×القاعدة ×الارتفاع =1/2×3×6 =9سم²
ونرشح لكم قراءة موضوع ما هي مساحة المثلث؟ وكيفية حساب محيط المثلث: ما هي مساحة المثلث؟ وكيفية حساب محيط المثلث
وبذلك نكون وضحنا ما هي المثلثات وأنواعها ، وكيفية حساب مساحة المثلث، و مساحة المثلث مختلف الأضلاع بصفة خاصة بطرق مختلفة، والقوانين المستخدمة في ذلك وأمثلة توضيحية للتدريب على حسابها.
